
1 引言
光学显微镜旨在对肉眼无法看到的物体,产生放大的视觉或摄影(包括数字)图像,不仅包括具有物镜和聚光镜的多镜头(复合显微镜)设计,还包括简单的单镜头仪器(通常是手持式),如摄影用放大镜或普通放大镜。
操作显微镜是可以轻易学会的技能,尽管一开始复杂的开关、过滤器、旋钮、滑块、目镜铭文和物镜可能令人困惑,但在短时间内可以理解它们。一旦新手开始理解和应用技术的基本原则,加上多年的实践和学习、初学者最终都会成为显微镜专家。
很多用户依赖于眼睛的观察,因此了解显微镜和人眼之间的关系是至关重要的。无论技术如何进步,人眼(与大脑结合的视觉检测器)是有史以来最有效的图像处理系统。在成像速度和分辨率方面,没有任何设备能与人眼的能力相媲美。然而,现代相机的工作原理与眼睛的结构和运作密切相关(见图1)。
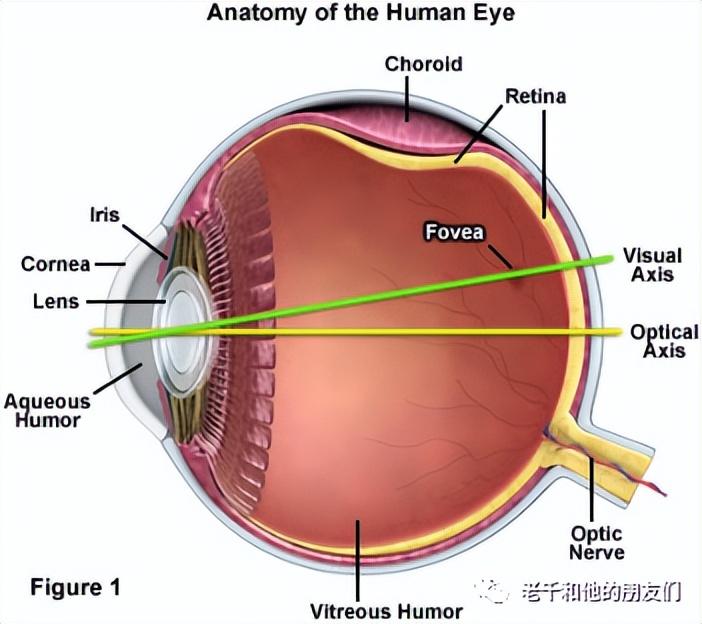
图1 人眼构造示意图
与肌肉调节的晶状体一起,角膜的弯曲表面将光学图像投射到视网膜(探测器)上。入射光亮度的高低是在特定肌肉的控制下,通过虹膜的可变直径(很像光学隔膜)来控制的。锐利的图像由灵活的透镜产生,其焦距由另一组肌肉改变,因此可以在大约20厘米和无限远的距离内对任何物体进行聚焦。图像本身在视网膜上被大约1.3亿个感光杆细胞(负责识别灰度)和700万个感光锥细胞(识别颜色)检测到,然后沿着最短的路径通过视神经传递到大脑。

图2 人眼的聚焦功能
图2可以说明人眼在不同距离上观察物体的适应性(30度观察角度),分别在50米的距离上观察一只飞鸭,和在25厘米的近距离上观察一只蝴蝶。由于眼睛的晶状体改变形状的能力有限,离眼睛极近的物体不能使它们的图像在视网膜上成焦点。例如,如果你想更仔细地观察植物茎部的细微毛细血管(见图3),你会从茎部切下一个薄片,放在显微镜载玻片上,用盖玻片保护它。
当你把植物茎部样品举到灯光下时,你会发现还有很多细节没有被发现。当我们试图在200米的距离上观察鸭子时,也会出现类似的情况。由于物体不能使它们的图像在视网膜上成焦点,在这么远的距离上无法识别鸟的翅膀中存在的许多细节。图3(b)展示了植物茎干的放大视图,以说明复合显微镜的威力。

图3 人眼无法观察到植物茎部细节
2 放大镜的概念
五百多年前,人们开发了简单的玻璃放大镜来帮助观察非常小的物体。这种仪器由一个或多个凸透镜(中心比周边厚)组成,使物体能够被置于物体和眼睛之间的放大镜聚焦。
这被称为简单显微镜,它们通过增加视网膜上的视觉角度的过程,以放大的方式在视网膜上显示图像。图4展示了一个简单的双凸透镜的工作原理示意图。尽管图像看起来与镜头在同一侧,但它不能被投射到屏幕上,这种图像被称为虚拟图像。在复式显微镜中,图像似乎漂浮在空间中,就在插入目镜的观察管顶部下方(在目镜固定光阑的水平)。
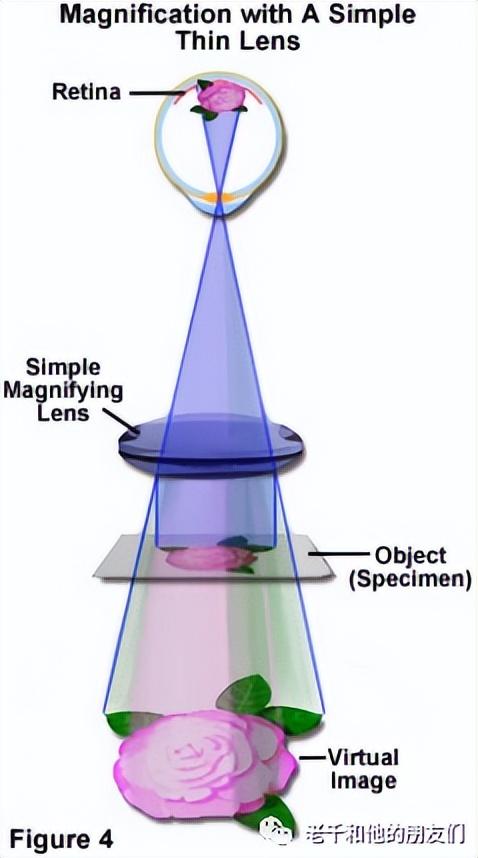
图4 简单的双凸透镜工作原理示意图
使用简单的双凸透镜,无法观察超过8倍或10倍的放大率。为了达到更高的放大率,我们必须使用复式显微镜,它最初是由荷兰的杨森兄弟和意大利的伽利略在16世纪初左右开发的。在其最简单的形式中,该仪器由两个串联的凸透镜组成。一个离物体较近的物镜,和一个离观察者眼睛较近的目镜。复式显微镜实现了两级放大,其中物镜将放大的图像投射到显微镜中,目镜将投射的图像进一步放大。总放大率等于物镜的放大率乘以目镜的放大率。
最早的复式显微镜受到了光学像差(包括色差和球差)的阻碍。这种缺陷是由于白光是由许多波长组成的,当光通过镜头的边缘时,它们不能与通过中心的光形成焦点。早期显微镜产生的图像往往是模糊的,带有彩色光晕,直到17世纪中期的镜头制造商发现,通过将两个具有不同色散的玻璃制成的镜头结合起来,可以减少或消除大部分色差。
现代显微镜通常有用于不同目的的可互换部件,并且有几个镜头一前一后地排列,从而使放大率达到2000倍或更高,能产生高清晰度和对比度的图像。

图5 现代显微镜的无限远色差校正光学系统(ICS)原理示意图。复杂的复合显微镜系统所产生的观察角度比直接观察的结果要大得多(图5(b)),即从大约25厘米的距离直接看到物体。
图5显示的现代显微镜的无限远色差校正光学系统(ICS)原理示意图,其特点是有一个管状透镜。在显微镜的光束路径中(图5(a)),物体被物镜记录下来,以平行的波阵或射线束投射到无限远处(从一个点出发的光线在物镜后面以直线、平行的方式前进)。
然后,管状透镜对平行光线束进行聚焦,产生一个位于目镜内前焦平面的放大的中间图像。目镜作为第二个放大镜,将中间图像转化为平行光线。这些平行束相交的区域被称为眼点,那是眼睛虹膜应该位于的地方。眼睛的角膜和晶状体将这些平行光线聚焦到视网膜上。
在选定的数值孔径(物镜角度孔径的正弦值乘以成像介质的折射率)下,显微镜呈现的放大图像的大小相当于人眼的分辨率极限,超过此点的进一步放大不会导致更精细的试样细节的分辨率。
物镜和目镜组合的有效总放大率范围由数值孔径定义。对于眼睛所能分辨的图像中的细节,有一个必要的最小放大率,这个值通常被设定为数值孔径的500倍(500xNA)。最大有效放大率通常被设定为数值孔径的1000倍(1000xNA)。这个限制是由衍射作用下强加在物镜上的光的波的性质决定的。超过这个值,放大率将不会产生额外有用信息,并且通常会导致图像退化。
这些基本放大原理是复合显微镜的操作和构造的基础。基于对这些原理的理解,导致了能够从低倍到高倍产生高质量图像的精密仪器的发展。
3 光镜图像的形成
在光学显微镜中,照明源的光通过聚光镜,然后通过试样时,一些光在其路径上不受干扰地通过试样,这种光被称为直射光、无偏移光或无衍射光,代表背景光。与试样相互作用的光是偏离的或衍射的。
衍射光与直射光形成二分之一波长(由试样本身引起的二分之一波长的相位差),使这种光在到达位于目镜固定光阑的中间像面时,与直射光产生干扰。目镜的眼透镜进一步放大这个图像,最后投射到视网膜、照相机的胶片平面或光敏数字图像传感器的表面。

图1 光镜中图像形成原理示意图
直射光由物镜投射,在目镜的光阑处均匀地散布在整个像面上。衍射光在物镜后焦平面上产生干扰(见图1),并在同一像平面上的各个局部位置聚焦,在那里,衍射光引起干扰并降低强度,从而产生了包含从非常暗到非常亮的各种灰度值的图案。这些明暗图案就是我们所认识的的图像。
为了帮助理解图像形成的基本原理,用已知的周期性结构的物体(类似的密布暗线的光栅)作为参考。将细尺光栅放在显微镜平台上,先用10倍和40倍的物镜将其对准。取下目镜,在其位置上插入一个相位镜,这样就可以观察到物镜的后焦平面。如果聚光器的光圈光阑大部分关闭,在物镜的后面会出现一个明亮的白色中心光点,这就是光圈光阑的影像。在中心光斑的左右两侧,将出现一系列衍射光谱,每个光谱在最接近中心光斑的部分上都被染成蓝色,在离中心光斑最远的部分被染成红色(如图2所示)。这些彩色光谱的强度根据光谱距离中心光斑的远近而减少。

图2 光镜中得衍射光谱
那些落在物镜外的衍射光谱比那些靠近中心点的衍射光谱更暗。图2中说明的衍射光谱是用三种不同的物镜放大率拍摄的。在图2(b)中,在10倍物镜的后焦平面上的可见衍射图案包含两个衍射光谱。如图2(a)所示,如果将光栅从平台上移开,这些光谱就会消失,只剩下孔径光阑的中心图像。如果重新插入光栅,光谱再次出现。
如果用40倍物镜检查线状光栅(如图2(c)),在中央孔径的左边和右边会出现几个衍射光谱。当放大倍数增加到60倍或63倍时(并假设它的数值孔径高于40倍物镜),在40倍物镜下可见的光谱的左右两边会出现几个额外的光谱(见图2(d))。
因为当光栅被移除时,彩色光谱消失了,所以可以假设是试样本身影响了通过的光线,从而产生了彩色光谱。此外,如果孔径光阑非常小,我们将观察到高数值孔径的物镜比低数值孔径的物镜,更能捕捉这些彩色光谱。这两个概念对理解图像形成的非常关键。
中心光斑(聚光镜光阑的图像)代表了直射或未偏离的光线穿过试样(如图3(b)所示),它被称为0阶或Zeroth阶。在零阶两侧的光圈光阑较暗的图像分别称为第1、2、3、4等阶,如图3(a)中的模拟衍射图案所示,这将在40倍物镜的后焦平面观察到。在这种情况下,所有捕获的阶数代表了在物镜后焦平面上看到的线光栅的衍射图案。

图3 直射光线和衍射光线形成图像示意图
孔径光阑上较暗的衍射图像是由衍射波阵引起的,在线光栅的每个开口处呈扇形散开(图3(b))。蓝色波长的衍射角度比绿色波长小,而绿色波长的衍射角度比红色波长小。在物镜的后焦平面,来自每个狭缝的蓝色波长相互影响,产生每个光谱或阶次的衍射图像(蓝色区域),红色和绿色区域(图3(a))的间距稍远。当这些颜色的衍射波长有二分之一的偏差时,这些波就会相互干扰,产生光谱或阶数之间的暗区。

图4 线光栅与网格的衍射图案
如图4(a-c)所示,线光栅的间距越近,物镜捕获的光谱就越少。图4(a)中的衍射图案是由40倍的物镜对图4(b)中线光栅的下部进行成像,其中狭缝更近。在图4(c)中,物镜聚焦于线状光栅的上部(图4(b)),那里狭缝相距较远,物镜捕捉到了更多的光谱。
直射光和来自高阶衍射最大值的光被物镜聚焦,在目镜的固定光阑处的中间像面中形成一个图像。在这里,直射光和衍射光相互干扰,从而重组为真实的、倒置的图像,由目镜看到并进一步放大。这在图4(d)至图4(g)中用两种类型的衍射光栅进行了说明。
图4(d)中说明的方形网格代表了通过物镜的全孔径看到的网格的正视图像(实际上是通过目镜观察到的通常的图像)。从这个网格中得到的衍射图案显示为在物镜的后焦平面看到的图像(图4(e))。同样,六边形排列的网格的正视图像(图4(f))产生相应的六边形排列的一阶衍射图案的图像(图4(g))。
4 衍射光和分辨率
显微镜形成图像形成的概念主要是由19世纪德国著名的显微镜和光学理论家恩斯特-阿贝提出的。根据阿贝的说法(他的理论在目前仍被广泛接受),如果物镜捕捉到2阶光,如0阶光和至少1阶衍射光,就可以看到细节。进入物镜的衍射阶数越多,图像就越能准确表达原始物体。此外,如果在物镜前透镜和盖玻片顶部之间的空间使用比空气折射率更高的介质(如浸泡油)(如图5(a)中干燥物镜所示),则衍射阶数的角度会减少,衍射光的扇形会被压缩。因此,油浸物镜可以捕获更多的衍射环,并产生更好的分辨率(图5(b))。
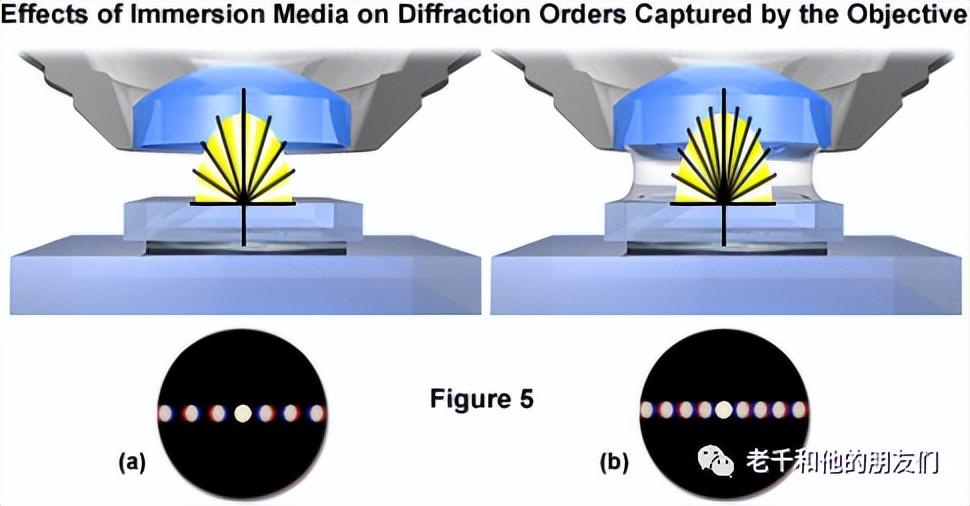
图5 浸没物镜工作原理示意图,可以捕获更多得的衍射环
此外,由于蓝光的衍射角度比绿光或红光小,当波长在可见光光谱的蓝色区域时,一个给定孔径的镜头可以捕获更多的光阶。这两个原则解释了经典的瑞利方程式,该方程式经常被引用为计算显微镜中点对点分辨率的基础。
d(分辨率)=1.22(λ/2NA)(1)
其中d是两个相邻颗粒之间的空间(仍然允许颗粒被视为独立的),λ是照明的波长,NA是物镜的数值孔径。
假设显微镜还配备了一个与物镜数值孔径相同的聚光镜(如果没有聚光镜,分辨率将是一半)。进入物镜的高衍射阶数越多,可清楚分离或分辨的细节就越小。这就是使用高数值孔径物镜来检查样品小的细节的价值所在。同样,使用的可见光的波长越短,分辨率越高。这些想法解释了为什么高数值孔径透镜可以在蓝光中分离出更小的细节。
在物镜的后面放置一个不透明的掩膜,可以阻挡最外层的衍射光阶。这要么降低了光栅线的分辨率,要么完全破坏了分辨率。因此,通常要注意不要将聚光器的光阑关闭到建议的物镜孔径的三分之二以下。
如果物镜不能捕捉到一个以上的衍射阶数,就会导致图像无法分辨。物镜将直射光和衍射光投射到目镜光阑的像面上,形成小的圆形衍射图案,称为艾里盘(如图6所示)。与低数值孔径物镜相比,高数值孔径物镜可以捕捉到更多的衍射光,并产生更小的圆盘尺寸。在图6中,艾里盘的尺寸从图6(a)到图6(c)稳步下降。图6(a)和(b)中较大的圆盘尺寸是由数值孔径较小的物镜产生的,而图6(c)中非常尖锐的艾里圆盘是由数值孔径非常大的物镜产生的。
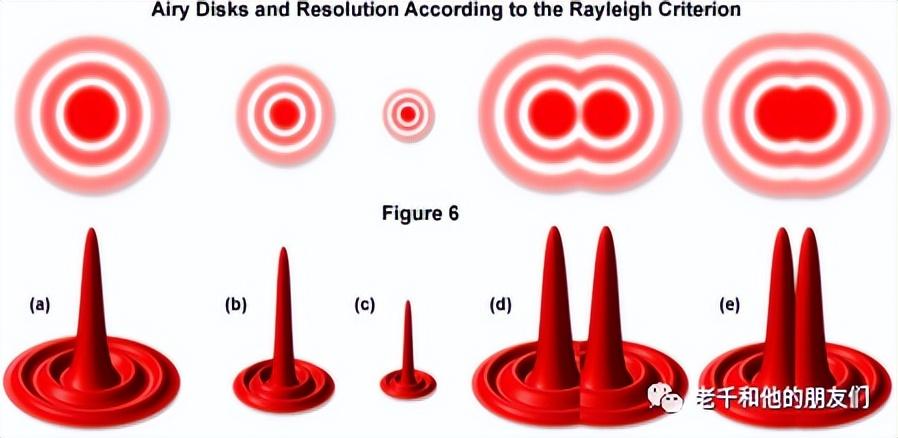
图6 艾里盘和瑞利判据(分辨率)
当两个圆盘靠得很近,以至于它们的中心亮点严重重叠时,这些重叠的圆盘所代表的两个细节就不能被分辨或分离,从而显示为一个整体(如图6(e)所示)。与此相反,图6(d)中所示的Airy盘的距离刚刚好,足以被分辨出来。
需要记住的基本原则是,直射光和衍射光的结合(或对直射光或衍射光的操纵)在图像形成中是至关重要的。这种操作的关键位置是物镜的后焦平面和聚光镜的前焦平面。这一原则是光学显微镜中大多数对比度改进方法的基础。更重要的是,它在高倍率的小细节尺寸接近光的波长时具有特殊意义。恩斯特-阿贝是发展这些概念以解释吸光或振幅的图像形成的先驱。


















