我们知道怎么定义一个不定积分:
如下图,如果f(t)在(a,b)上是连续可积的,在常数a和f(t)保持不变的情况下,我们就可以通过以下方法在(a,b)上得到一个全新的函数,这也是很常见的
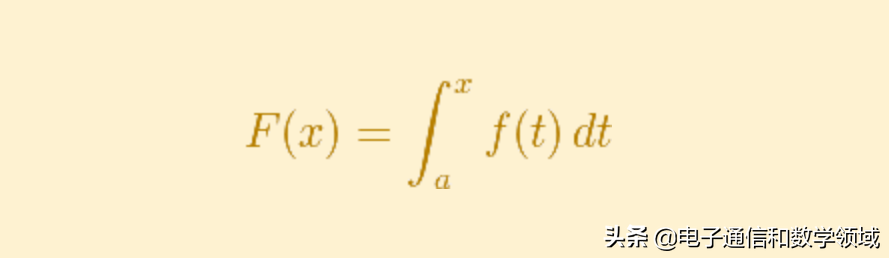
我们称它为特殊情况下的不定积分,因为它的上限是一个未知数,我们在这里引用这种形式,是有好处的,继续往下看
如果f(x)是在此区间下是一个正值,f (x)就是一个有关面积的函数。这也是牛顿-莱布尼兹公式的本质原理,也是微积分入门的必要基础
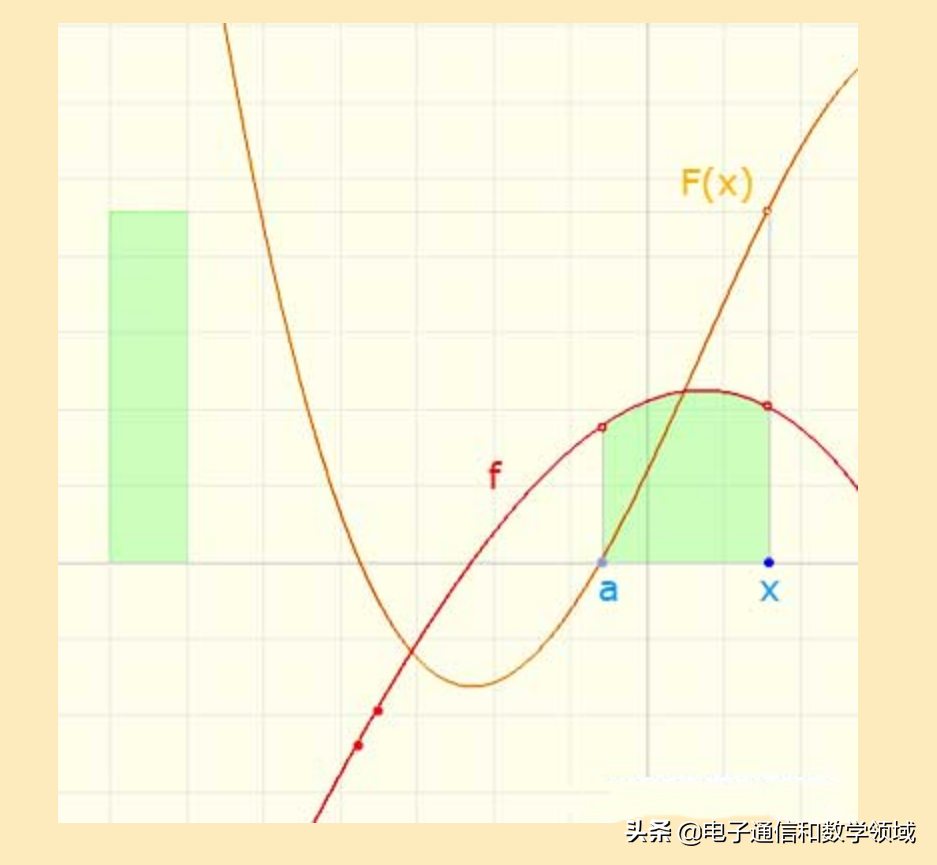
此处的F(x)只依赖于下限常数a,因为选择不同的a值就会得到不同的函数F(x),但是不同函数F(x)之间的差与x是没有关系的,它们只相差一个常数
如果f(x)在某个区间内为正,则F(x)(F(x)为面积)会不断增加,因为F(x)的导数就是f(x),即F(x)所表示的面积和F(x)面积下的导数f(x)一一对应,如下图所示
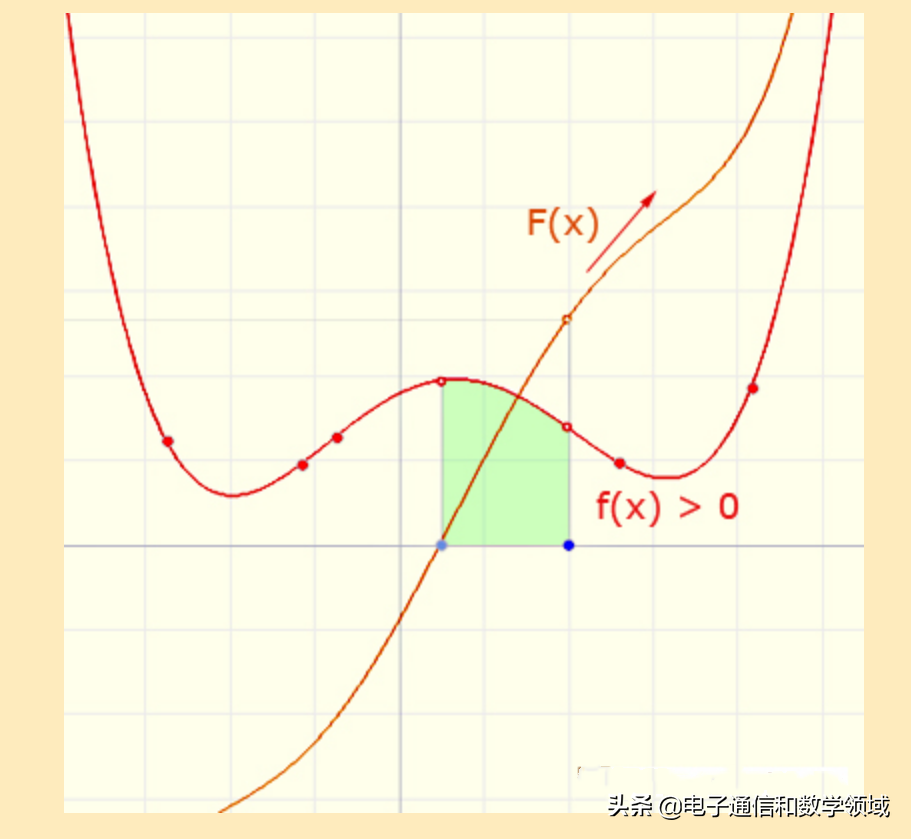
如果f(x)在某个区间内为负,则F(x)(F(x)为面积)会不断减小,同理:F(x)的导数正好与f(x)的函数图形相对应
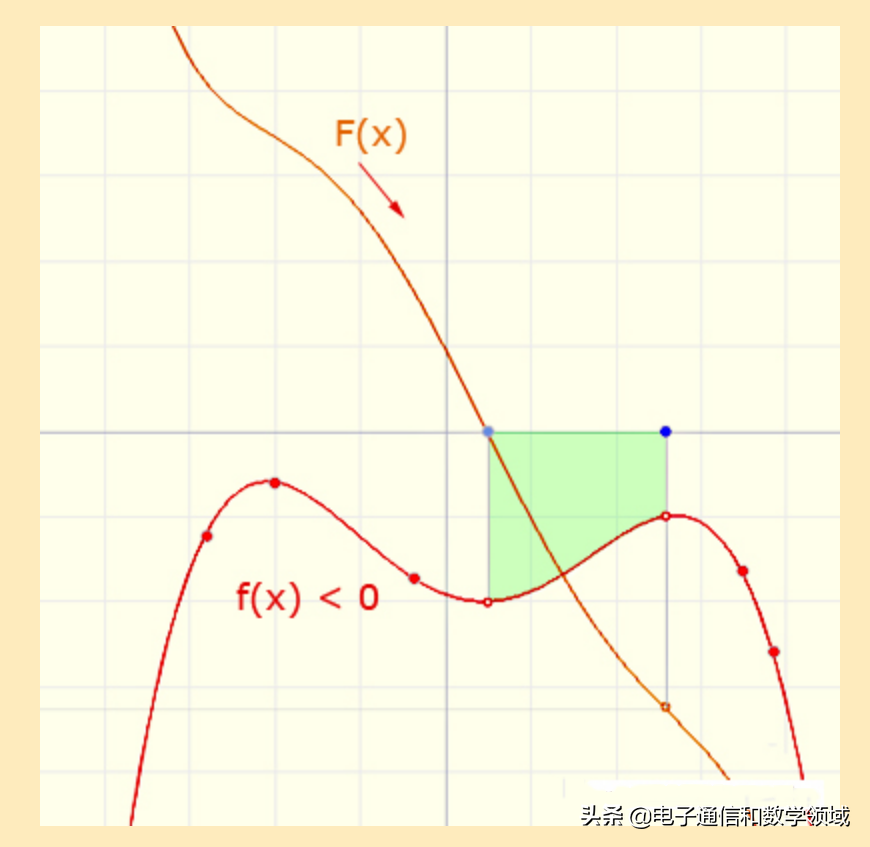
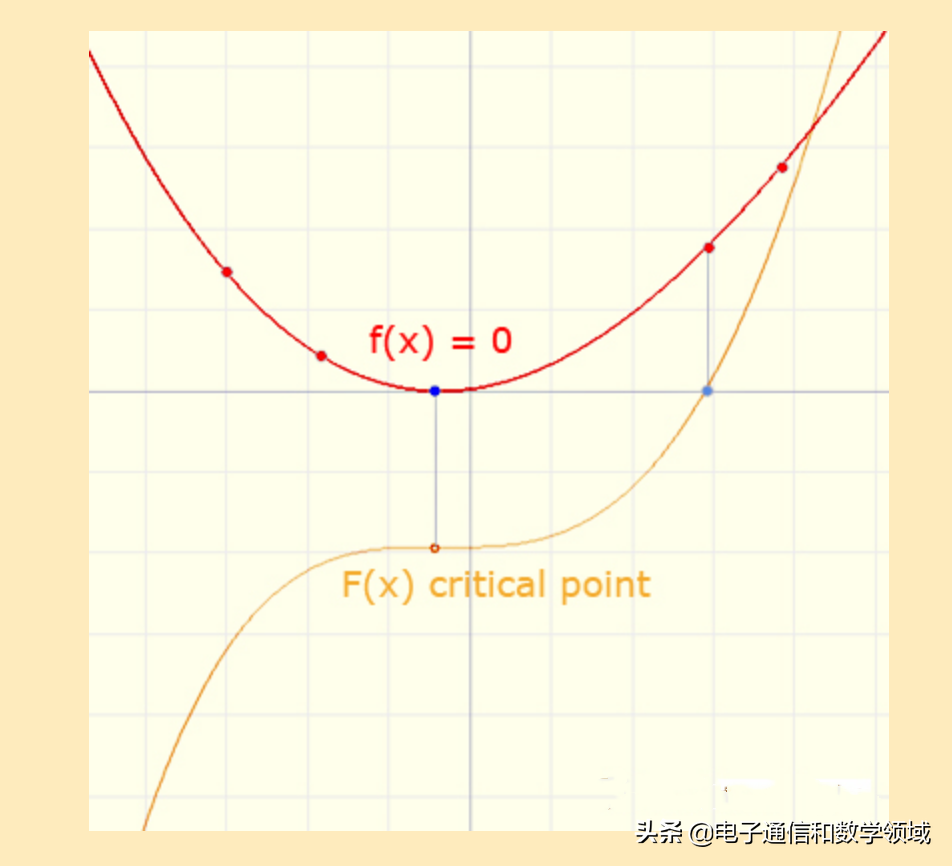
假如(x)= 0,则x就是F的临界点。这个临界点就是书本上所描述的极大值和极小值
如下图所示:f(x)=0时,与其相对应的F(x)取极小值,如果F(x)的二阶导数为0,该点就是F(x)的拐点。拐点就是凹凸的分界点,即f(x)的斜率等于0,下面的图形非常明显的表达了这一观点
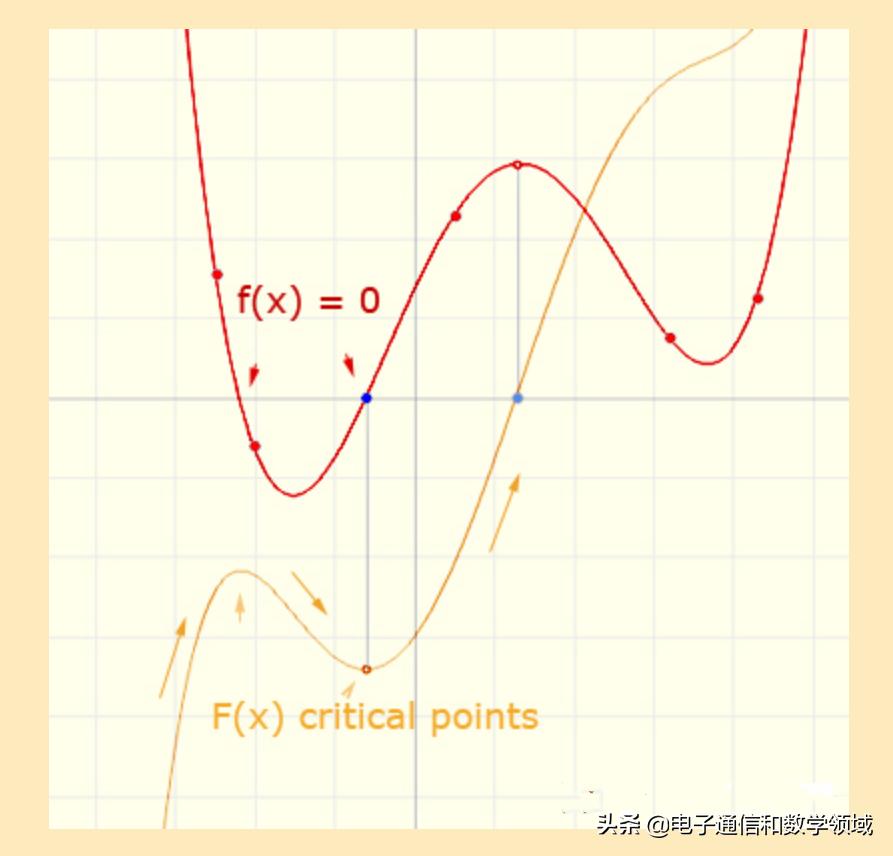
如果f(x)的图形是一个抛物线形状,那么与它相对应的反导数F(x)图形就是一个三次函数曲线
而拐点正好是f(x)的极小值,如下图f(x)导数等于0处的坐标值就是F(x)的拐点