
长方形的面积=长×宽,正方形的面积=边长×边长。掌握并能运用这两个面积公式,就能计算它们的面积。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。这就需要我们切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法,使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答。
例1 已知大正方形比小正方形边长多2厘米,大正方形比小正方形的面积大40平方厘米。求大、小正方形的面积各是多少平方厘米?

分析
从图中可以看出,大正方形的面积比小正方形的面积大出的40平方厘米,可以分成三部分,其中A和B的面积相等。
因此,用40平方厘米减去阴影部分的面积,再除以2就能得到长方形A和B的面积,再用A或B的面积除以2就是小正方形的边长。求到了小正方形的边长,计算大、小正方形的面积就非常简单了。
(40-2×2)÷2=18(平方厘米)
18÷2=9(厘米)
小正方形9×9=81(平方厘米)
大正方形(9+2)×(9+2)=121(平方厘米)
例2 一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形,其中三个长方形的面积如下图所求,求第四个长方形的面积。
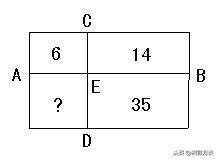
分析
因为AE×CE=6,DE×EB=35,
把两个式子相乘AE×CE×DE×EB=35×6,
而CE×EB=14,
所以AE×DE=35×6÷14=15。
例3 把20分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差40平方分米,大正方形的面积是多少平方分米?
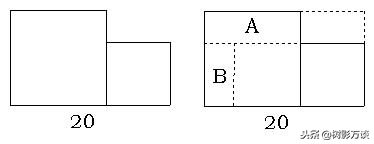
分析
我们可以把小正方形移至大正方形里面进行分析。两个正方形的面积差40平方分米就是图中的A和B两部分,如图。
如果把B移到原来小正方形的上面,不难看出,A和B正好组成一个长方形,
此长方形的面积是40平方分米,
长20分米,宽是40÷20=2(分米),即大、小两个正方形的边长相差2分米。
因此,大正方形的边长就是(20+2)÷2=11(分米),
面积是11×11=121(平方分米)
例4 有一个正方形ABCD如下图,请把这个正方形的面积扩大1倍,并画出来。

分析
由于不知道正方形的边长和面积,所以,也没有办法计算出所画正方形的边长或面积。
我们可以利用两个正方形之间的关系进行分析。
以正方形的四条边为准,分别作出4个等腰直角三角形,如图中虚线部分,显然,虚线表示的正方形的面积就是原正方形面积的2倍。
例5 有一个周长是72厘米的长方形,它是由三个大小相等的正方形拼成的。一个正方形的面积是多少平方厘米?
分析
三个同样大小的正方形拼成的长方形,它的周长是原正方形边长的8倍,正方形的边长为72÷8=9(厘米),一个正方形的面积就是9×9=81(平方厘米)。


















