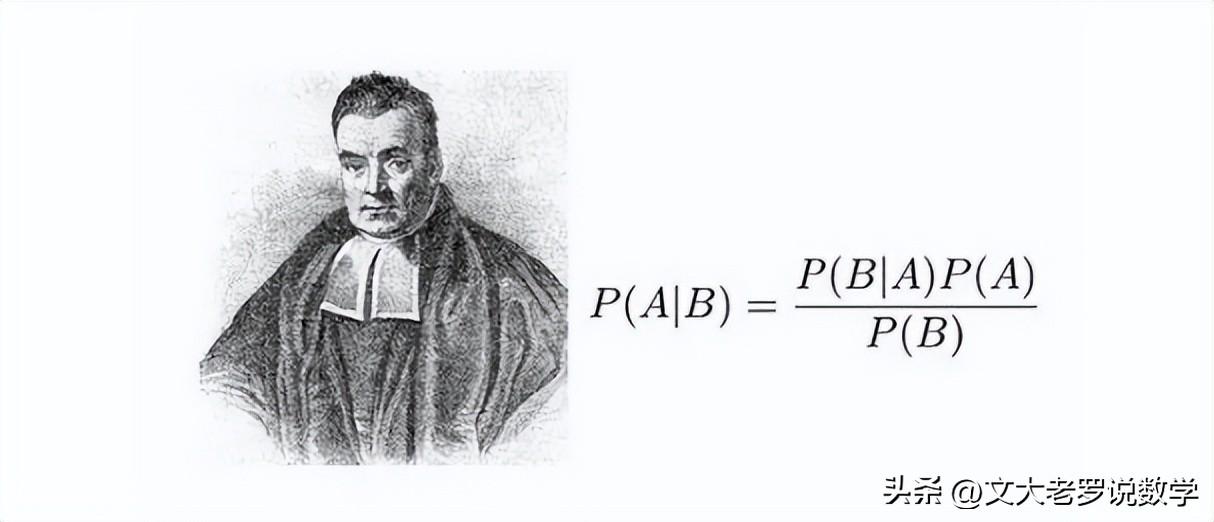概率是高中数学中的一个重要专题,它是研究随机事件发生可能性大小的数学工具。在学习概率的过程中,我们需要掌握一些基本概念和计算方法,这些内容也是高考数学中的重点。

一、概率的定义和性质
1、概率的定义:概率是衡量随机事件发生可能性大小的数值,取值在0到1之间。当概率等于0时,表示事件不可能发生;当概率等于1时,表示事件一定发生。
2、概率的性质:
(1)非负性:概率的取值不能小于0。
(2)规范性:所有事件的概率和为1。
(3)可加性:对于两个互斥事件(即不可能同时发生的事件),其概率的和等于各自概率之和。
二、概率的计算方法
1、古典概型:在古典概型中,样本空间是有限的,每个样本点出现的可能性相同。计算概率时,可以采用计数的方法,将样本点数除以总样本点数,得到所求事件的概率。
2、几何概型:在几何概型中,样本空间是无限的,每个样本点出现的可能性相同。计算概率时,可以采用测量的方法,将所求事件的长度(面积或体积)除以总样本空间的长度(面积或体积),得到所求事件的概率。
三、概率的应用
1、概率分布:在概率论中,随机变量的取值概率之间的关系称为概率分布。常见的概率分布有离散型分布和连续型分布,如二项分布、正态分布等。
2、条件概率:在已知某些信息的情况下,事件发生的概率称为条件概率。条件概率的计算方法为:在已知条件下的事件发生的概率除以在所有情况下的该事件发生的概率。
3、独立性:若两个事件之间没有影响,则称它们是独立的。在独立的情况下,事件的概率乘法公式成立,即两个独立事件同时发生的概率等于各自发生概率的乘积。
4、贝叶斯公式:贝叶斯公式用于在已知某些信息的情况下,估计未知变量的概率分布。公式为:在已知条件下的事件发生的概率乘以该条件下事件发生的先验概率,再除以在所有情况下的该事件发生的概率。
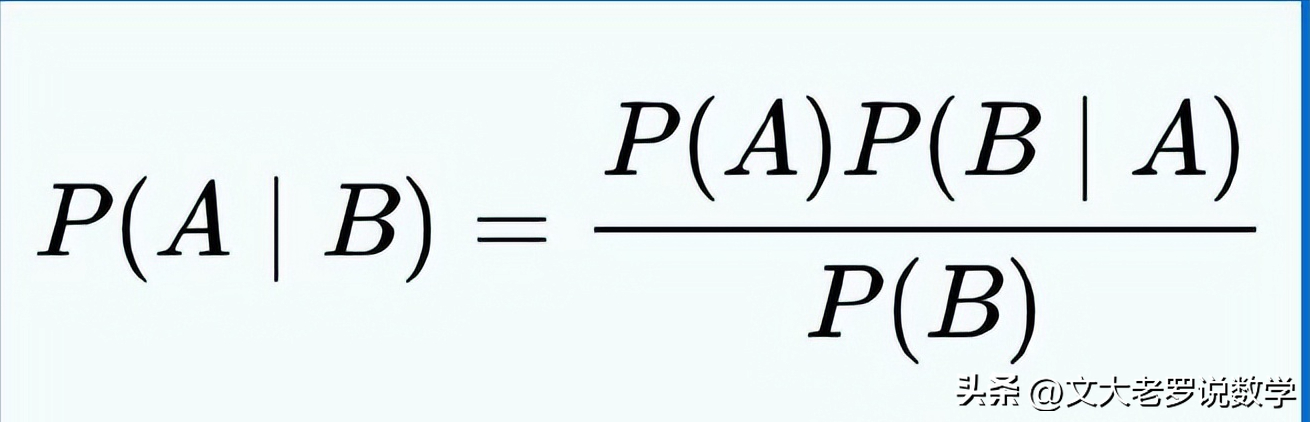
四、概率的变化规律
1、概率的周期性变化:在一些情况下,概率的取值呈现出周期性变化。例如,抛掷硬币正面朝上的概率在一个较长时间内呈现出周期性变化。
2、概率的非周期性变化:在一些情况下,概率的取值呈现出非周期性变化。例如,投掷一个六面体的骰子,其每个面朝上的概率呈现出非周期性变化。
五、总结
通过以上讲解,我们可以了解到概率的基本概念、计算方法和应用领域。概率是研究随机事件的重要工具,它有着广泛的应用。在实际问题中,我们需要根据具体情境选择合适的概率模型进行计算和分析。同时,我们还需要了解概率的变化规律,这将有助于我们更好地理解和解释实际现象。在掌握这些知识点的基础上,我们将能够更好地应对与概率相关的数学问题。